CALCULO DE ÁREAS
 Sea f una función cuyo dominio esta en el intervalo cerrado [a, b], tal que f(x) ≥ 0 para x ∈ [a, b]. Sea R la región plana limitada por las gráficas de las ecuaciones: y = f(x), y = 0 (eje x), x = a, x =b.
 Área de una región comprendida entre dos curvas.
Sean f y g dos funciones con dominio en el intervalo [a, b], tales que f(x) ≥ g(x) para x ∈ [a, b]. Vamos a determinar cual es el área de la región R limitada por las gráficas de y = f(x), y = g(x), x = a, x = b que se muestra a continuación: Construimos un conjunto de rectángulos tales que la suma de sus áreas sea una aproximación al área de R.

ÁREA BAJO UNA CURVA

Teorema fundamental del cálculo. Si una función es continua en un intervalo cerrado [a, b], entonces
la integral .
 F (b) – F (a).
 En donde F es cualquier función tal Por el teorema fundamental del cálculo sabemos que si entonces existe una integral definida al área bajo la curva descrita por ejemplo .Dada la función y= 4, encontrar el área que se encuentra bajo la recta en el intervalo [2, 5]. 4dx = aplicamos la fórmula 2. 4 dx = aplicamos la fórmula = evaluamos los límites. 4(5)+ C– [4(2) +C]= cancelamos las constantes. 20+ C – 8–C= 20 – 8= 12u2
Nota: En una integral definida la constante de integración desaparece al efectuar la diferencia de los límites de integración. Área bajo la curva y la integral definida. Teorema fundamental del cálculo. Si una función es continua en un intervalo cerrado [a, b], entonces la integral  de  F(b) – F(a) Cualquier función tal que F(x)= para toda Por el teorema fundamental del cálculo sabemos que si f es una función continua en [a, b], entonces existe una integral definida . El resultado de dicha integral será igual descrita por f(x) representada en un plano.
LONGITUD DE ARCO
En matemática, la longitud de arco, también llamada rectificación de una curva, es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. Históricamente, ha sido difícil determinar esta longitud en segmentos irregulares; aunque fueron usados varios métodos para curvas específicas, la llegada del cálculo trajo consigo la fórmula general para obtener soluciones cerradas para algunos casos.

Al considerar una curva definida por una función  y su respectiva derivada  que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:

LONGITUD DE UNA CURVA 

La idea para calcular la longitud de una curva contenida en el plano o en el espacio consiste en dividirla en segmentos peque˜nos, escogiendo una familia finita de puntos en C, y aproximar la longitud mediante la longitud de la poligonal que pasa por dichos puntos. Cuantos mas puntos escojamos en C, mejor ser´a el valor obtenido como aproximacion de la longitud de C.

Para que el centroide del cuerpo coincida con el centro de masa, el cuerpo debe tener densidad uniforme o una distribución de materia que presente ciertas propiedades, tales como la simetría.

CALCULO INTEGRAL 
UNIDAD 3
DELMAN DARINEL CRUZ MARROQUIN

APLICACIÓN DE LAS INTEGRALES 
La integral definida es un método rápido para calcular áreas volúmenes longitudes etc.

APLICACIONES
CALCULO DE ÁREAS PLANAS.
es un generalizador del proceso del calculo de áreas. ahora bien el área de un recinto es siempre positivo mientras que la integral puede ser positivo y negativo o nula.
CALCULO DE VOLÚMENES
al introducir la integración el área solamente es una de las muchas aplicaciones de la integral definida orta aplicación importante lo tenemos en uso para calcular el volumen de un solido tridimensional.
si una región de un plano gira alrededor de un eje de ese mismo plano se obtiene una región tridimensional llamada solido de una revolución.
ÁREA DE UNA SUPERFICIE DE UNA REVOLUCIÓN
si se gira la gráfica de una función continua alrededor de una recta la recta resultante se conoce como superficie de revolución.
para calcular el área de una superficie de revolución usamos  la formula de la superficie lateral de un tronco de cono circular recto.






Longitud de una curva
En matemática, la longitud de arco, también llamada rectificación de una curva, es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. Históricamente, ha sido difícil determinar esta longitud en segmentos irregulares; aunque fueron usados varios métodos para curvas específicas, la llegada del cálculo trajo consigo la fórmula general para obtener soluciones cerradas para algunos casos.Al considerar una curva definida por una función  y su respectiva derivada  que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:

(1)

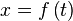En el caso de una curva definida paramétricamente mediante dos funciones dependientes de t como  e 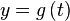, la longitud del arco desde el punto  hasta el punto  se calcula mediante:

(2)

Área bajo una curva
La formulación del área bajo una curva es el primer paso para desarrollar el concepto deintegral. El área bajo la curva formada por el trazo de la función f(x) y el eje x se puede obtener aproximadamente, dibujando rectángulos de anchura finita y altura f igual al valor de la función en el centro del intervalo.
Definición: Sí f es continua y no negativa en un intervalo cerrado , el área de la región limitada por la gráfica de f, el eje x y las rectas verticales viene dada por:
ÁREA = ∫ f(x)dx
Longitud de una curva.
Sabemos lo que significa la longitud de un segmento recto. En particular, si tenemos dos puntos del plano a=(a1y a2) y B = (b1y b2,) la longitud del segmento AB es, según el teorema de pitagoras.

Cálculo de los centroides

En Matemáticas, los centroides de una figura bidimensional se refieren al punto en el cual todas las líneas de la figura correspondiente se intersectan unas con otras de tal manera que dividen la figura en dos partes iguales en los momentos equivalentes.

Asimismo, la definición puede ser ampliada y se vuelve aplicable un objeto n-dimensional.

Si se establece físicamente, un centroide se refiere al centro del objeto geométrico.

Por lo tanto, al calcular el centroide de una figura en particular, sólo el área de la figura geométrica se toma en cuenta. Por este motivo, el centroide también se denomina como centro geométrico.

El cálculo del centroide es una de las aplicaciones principales de las integrales.

Centroides por integración. El centroide de un área limitada por curvas analíticas (curvas definidas por ecuaciones algebraicas) por lo general se determina evaluando las integrales  ∫ x A = x dA integral     A y = y dA