DELMAN DARINEL CRUZ MARROQUIN
CALCULO INTEGRALUNIDAD 4
SERIE GEOMÉTRICA:
En matemática, una serie geométrica es una serie en la cual la razón entre los términos sucesivos de la serie permanece constante.
Por ejemplo la serie
es geométrica, pues cada término sucesivo se obtiene al multiplicar el anterior por  .
.
 .
.
RAZÓN COMÚN:
Los términos de una serie geométrica forman una progresión geométrica, es decir que la razón entre términos sucesivos permanece constante.
El comportamiento de los términos depende de la razón común r.
- Si
 los términos decrecen y se acercan a cero en el límite. En tal caso, la serie converge.
los términos decrecen y se acercan a cero en el límite. En tal caso, la serie converge. - Si
 los términos de la serie se incrementan en magnitud. La suma de los términos también aumenta y la serie no tiene suma. La serie diverge.
los términos de la serie se incrementan en magnitud. La suma de los términos también aumenta y la serie no tiene suma. La serie diverge.
La suma de una serie geométrica será finita siempre y cuando los términos se aproximen a cero; a medida que se acercan al cero, las cantidades se vuelven insignificante mente pequeñas, permitiendo calcular la suma sin importar el hecho que la serie sea infinita. La suma puede ser obtenida utilizando las propiedades auto similares de la serie.
FORMULA:
Para  , la suma de los primeros n términos de una serie geométrica es:
, la suma de los primeros n términos de una serie geométrica es:
 , la suma de los primeros n términos de una serie geométrica es:
, la suma de los primeros n términos de una serie geométrica es:
donde a es el primer término de la serie y r la razón común.
Ejemplo:
Dada la suma de la serie geométrica:
La razón común de esta serie es 2/3. Multiplicando por 2/3 cada término, se obtiene:
Esta nueva serie es como la original excepto por el primer término que falta. Retándolas, se obtiene:
 , por lo que
, por lo que  .
.
Una técnica similar puede utilizarse al evaluar cualquier expresión auto similar.
CONVERGENCIA:
La serie geométrica real de término inicial  no nulo y de razón
no nulo y de razón  es convergente si y solamente si
es convergente si y solamente si  . En tal caso, su suma vale:
. En tal caso, su suma vale:
 no nulo y de razón
no nulo y de razón  es convergente si y solamente si
es convergente si y solamente si  . En tal caso, su suma vale:
. En tal caso, su suma vale: DEFINICIÓN DE SERIE:
DEFINICIÓN DE SERIE:
Una serie es la suma indicada de los términos de una sucesión.
Así, de las sucesiones anteriores obtenemos las series
1+4+9+16+25
Cuando el numero de términos es limitado, se dice que la sucesión o serie es finita. Cuando el numero de términos es ilimitado, la secesión o serie se llama una sucesión infinita o una serie infinita.
Así, de las sucesiones anteriores obtenemos las series
1+4+9+16+25
Cuando el numero de términos es limitado, se dice que la sucesión o serie es finita. Cuando el numero de términos es ilimitado, la secesión o serie se llama una sucesión infinita o una serie infinita.
El termino general o termino enésimo es una expresión que indica la ley de la formación de los términos
SERIE FINITA:
Una serie numérica es un conjunto especial de números que se forma ordenadamente siguiendo determinada ley o condición, así por ejemplo.
2, 4, 6, 8, 10, 12, 14
2, 4, 8, 16, 32, 64,....
1, 1/2, 1/3, 1/4, 1/5
3, 6, 10, 12, 14, 20
Cuando la sucesión tiene un último término se dice que la sucesión es finita.
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de cauchy.
Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
serie Infinita.
Es un arreglo ordenado de números reales, uno para cada entero positivo. Mas formal mente una sucesión infinita es una función cuyo dominio es el conjunto de enteros positivos y cuyo rango es un conjunto de números reales. Podemos indicar una sucesión mediante a1 ,a2 ,a3,...., simplemente por {an}
Se puede especificar una sucesión dando suficientes términos iniciales para establecer un patrón como en
1, 4, 7, 10, 13, ....
mediante una formula explicita para el n-enésimo termino, como en
an = 3n-2, n ≥ 1
por definición y la fórmula binomial.
TIPOS DE SERIES:
Sumas parciales:
Para cualquier sucesión matemática  de números racionales, reales, complejos, funciones, etc., la serie asociada se define como la suma formal ordenada:
de números racionales, reales, complejos, funciones, etc., la serie asociada se define como la suma formal ordenada:
 de números racionales, reales, complejos, funciones, etc., la serie asociada se define como la suma formal ordenada:
de números racionales, reales, complejos, funciones, etc., la serie asociada se define como la suma formal ordenada:
La sucesión de sumas parciales  asociada a una sucesión
asociada a una sucesión  está definida para cada
está definida para cada  como la suma de la sucesión
como la suma de la sucesión  desde
desde  hasta
hasta  :
:
 asociada a una sucesión
asociada a una sucesión  está definida para cada
está definida para cada  como la suma de la sucesión
como la suma de la sucesión  desde
desde  hasta
hasta  :
:
Muchas de las propiedades generales de las series suelen enunciarse en términos de las sumas parciales asociadas.
Convergencia:
Por definición, la serie  converge al límite
converge al límite  si y sólo si la sucesión de sumas parciales asociada
si y sólo si la sucesión de sumas parciales asociada 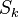 converge a
converge a  . Esta definición suele escribirse como
. Esta definición suele escribirse como
 converge al límite
converge al límite  si y sólo si la sucesión de sumas parciales asociada
si y sólo si la sucesión de sumas parciales asociada 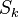 converge a
converge a  . Esta definición suele escribirse como
. Esta definición suele escribirse como
Las series de potencias:
Una serie del tipo:
a0 + a1 x + a2 x
2 + a3 x
3 +K+ an x n +K
ordenada por potencias enteras crecientes de la variable x y con coeficientes , , , , , . a0 a1 a2 K an K
constantes, independientes de x , recibe el nombre de serie de potencias.
A menudo consideramos la serie de potencias en una forma más general:
a0+a1(x-a)+a2(x-a)2+a3(x-a)3+....+an(x-a)n
SERIE DE TAYLOR:
Definición :
La serie de Taylor de una función f de números reales o complejos que es
infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de
potencias:
que puede ser escrito de una manera más compacta como la siguiente suma:
donde:
La derivada de orden cero de f es definida como la propia f y tanto (x − a)0 como  son ambos definidos como 1 (
son ambos definidos como 1 ( = 1).
= 1).
 son ambos definidos como 1 (
son ambos definidos como 1 ( = 1).
= 1).
BESSEL:
En matemática, las funciones de Bessel, primero definidas por el matemático Daniel Bernoulli y más tarde generalizadas por Friedrich Bessel, son soluciones canónicas y(x) de la ecuación diferencial de Bessel:
donde  es un número real o complejo. El caso más común es cuando
es un número real o complejo. El caso más común es cuando  es un entero
es un entero  , aunque la solución para
, aunque la solución para  no enteros es similar. El número
no enteros es similar. El número  se denomina orden de las funciones de Bessel asociadas a dicha ecuación.
se denomina orden de las funciones de Bessel asociadas a dicha ecuación.
 es un número real o complejo. El caso más común es cuando
es un número real o complejo. El caso más común es cuando  es un entero
es un entero  , aunque la solución para
, aunque la solución para  no enteros es similar. El número
no enteros es similar. El número  se denomina orden de las funciones de Bessel asociadas a dicha ecuación.
se denomina orden de las funciones de Bessel asociadas a dicha ecuación.
Dado que la ecuación anterior es una ecuación diferencial de segundo orden, tiene dos soluciones lineal mente independientes.
Aunque  y
y 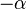 dan como resultado la misma función, es conveniente definir diferentes funciones de Bessel para estos dos parámetros, pues las funciones de Bessel en función del parámetro
dan como resultado la misma función, es conveniente definir diferentes funciones de Bessel para estos dos parámetros, pues las funciones de Bessel en función del parámetro  son funciones suaves casi doquiera. Las funciones de Bessel se denominan también funciones cilíndricas, o armónicos cilíndricos porque son solución de la ecuación de La place en coordenadas cilíndricas.
son funciones suaves casi doquiera. Las funciones de Bessel se denominan también funciones cilíndricas, o armónicos cilíndricos porque son solución de la ecuación de La place en coordenadas cilíndricas.
 y
y 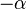 dan como resultado la misma función, es conveniente definir diferentes funciones de Bessel para estos dos parámetros, pues las funciones de Bessel en función del parámetro
dan como resultado la misma función, es conveniente definir diferentes funciones de Bessel para estos dos parámetros, pues las funciones de Bessel en función del parámetro  son funciones suaves casi doquiera. Las funciones de Bessel se denominan también funciones cilíndricas, o armónicos cilíndricos porque son solución de la ecuación de La place en coordenadas cilíndricas.
son funciones suaves casi doquiera. Las funciones de Bessel se denominan también funciones cilíndricas, o armónicos cilíndricos porque son solución de la ecuación de La place en coordenadas cilíndricas.










 y su respectiva
y su respectiva  que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:
que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:![s = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx](https://upload.wikimedia.org/math/e/6/1/e61ceab68a8e7295fadd088701908963.png)

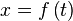 e
e 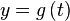 , la longitud del arco desde el punto
, la longitud del arco desde el punto  hasta el punto
hasta el punto  se calcula mediante:
se calcula mediante:![s = \int_{a}^{b} \sqrt{\left [ f' \left ( t \right ) \right ] ^2 + \left [ g' \left ( t \right ) \right ] ^2} \, dt](https://upload.wikimedia.org/math/8/4/8/8483f65e52e30ec4f0f24dfd8f6751a2.png)
