lunes, 21 de septiembre de 2015

QUE SON LAS FIGURAS AMORFAS:
Las figuras amorfas "son aquellas figuras que no tiene forma”. Es una curva o una figura de muchos lados distintos. Su principal finalidad es encontrar en una gráfica dada su área de la  parte de adentro de una figura donde se encuentra el punto dado de la figura amorfa.
NOTA DE SUMATORIA:
El sumatorio o la operación de suma, es un operador matemático que permite representar sumas de muchos sumando, n o incluso infinitos sumando. Se expresa con la letra griega sigma ( \Sigma , Σ), y se define como:
\sum_{i=m}^n x_i = x_m + x_{m+1} + x_{m+2} +\cdots + x_n
Esto se lee: «sumatorio sobre i, desde m hasta n, de x sub-i».
La variable i es el índice de suma al que se le asigna un valor inicial llamado límite inferior, m.
La variable i recorrerá los valores enteros hasta alcanzar el límite superior, n. Necesariamente debe cumplirse que:
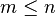
m \leq n
SUMA DE RIEMANN:
En matemáticas, la suma de Riemann sirve para calcular el valor de una integral definida, es decir, el área bajo una curva, este método es muy útil cuando no es posible utilizar el Teorema fundamental del cálculo. Estas sumas toman su nombre del matemático alemán Bernhard Riemann.
La suma de Riemann consiste en trazar un número finito de rectángulos dentro de un área irregular, calcular el área de cada uno de ellos y sumarlos. El problema de este método de integración numérica es que al sumar las áreas se obtiene un margen de error muy grande.
una función f:[D]\rightarrow\mathbb{R}
A) donde D I = [a, b] un intervalo cerrado contenido en D.
B) Un conjunto finito de puntos {x0, x1, x2, ... xn} tales que a = x0 < x1 < x2 ... < xn = b crean una partición de Ies un subconjunto de los números reales \mathbb{R}
P = {[x0, x1), [x1, x2), ... [xn-1, xn]}
C) Si P es una partición con n elementos de I, entonces la suma de Riemann de f sobre I con la partición P se define como
S = \sum_{i=1}^{n} f(y_i)(x_{i}-x_{i-1})

Función Primitiva:
Para algunas funciones de la forma f(x): X → Y, la primitiva se define como cualquier otra función la cual cuando es diferenciada nos da de nuevo la función original f(x).
Esto significa que f(x) es la derivada de su función primitiva o que la función primitiva es la integral de la presente función f(x).
Por tanto, podemos decir que si F(x) es la función primitiva de f(x) entonces F(x) + c es también su función primitiva para los valores distintos de c sin ningún pre-requisito para obtener a c.
Aquí F(x) + c representa a la familia de funciones primitivas. Al asignar distintos valores de c, obtenemos diferentes miembros de esta familia.
Geométricamente, estos miembros se pueden obtener al cambiar cualquiera de las curvas paralelas a ellos.
Existen muchos sinónimos para las funciones primitivas tales como primitiva integral, antiderivada, etc.
INTEGRAL IMPROPIA:
En cálculo, una integral impropia es el límite de una integral definida cuando uno o ambos extremos del intervalo de integración se acercan a un número real específico, a ∞, o a −∞. Además una integral definida es impropia cuando la función integrando de la integral definida no es continua en todo el intervalo de integración. También se pueden dar ambas situaciones.
Si la función f al ser integrada de a a c tiene una discontinuidad en c, especialmente en la forma de una asíntota vertical, o sic = ∞, entonces la integral
\int_a^c f(x)\,dx\,
Punto singular en el infinito.
Puede ser más conveniente redefinirla de la siguiente forma:
\lim_{b\to c^-}\int_a^b f(x)\,dx.\,




Publicado por en No hay comentarios:
Suscribirse a: Comentarios (Atom)